Números Octales

SISTEMA NUMÉRICO OCTAL

Algunos sistemas de cómputo antiguos utilizan los números octales para representar información binaria. El sistema de numeración octal emplea ocho símbolos: 0, 1, 2, 3, 4, 5, 6 y 7. Los números octales también se conocen como números base 8. La tabla de la figura 2.10 proporciona las representaciones en binario y octal de los números decimales 0 al 17. La ventaja del sistema octal es su utilidad en la conversión directa de un número binario de 3 bits. La notación octal se utiliza para representar números binarios.

 Figura 2.10

La conversión de números octales a binarios es una operación común cuando se utilizan ciertos sistemas de cómputo. Considere la conversión del número octal 678 (léase “seis siete base ocho”) a su equivalente binario. La figura 2.11 cada dígito octal se convierte a su equivalente binario de 3 dígitos. El número 6 en octal equivale a 110, mientras que el 7 equivale a 111. Combinando los grupos binarios obtenemos 678  = 1101112

Figura 2.11

Ahora invierta el proceso y convierta el número binario 100001101 en su equivalente octal. En la figura 2.12 se muestra el proceso a detalle. El número binario se divide en grupos de 3 bits (100 001 101) a partir del punto binario. Enseguida, cada grupo de 3 bits se traduce en su número octal equivalente. El ejemplo de la figura 2.12 demuestra que 1000011012 = 4158

Figura 2.12

Considere la conversión del número octal 4158 (léase “cuatro uno cinco base 8”) a su equivalente decimal. Los valores de las posiciones de los tres primeros lugares del número octal se muestran en la parte superior de la figura 2.13 y son 64, 8 y 1. Hay cinco 1 y un 8. Hay cuatro 64 que equivalen a 256. Se suma 5 + 8 + 256 = 26910. El ejemplo de la figura 2.13 muestra que 4158 = 26910

Figura 2.13 

Ahora invierta el proceso y convierta el número decimal 498 a su equivalente octal.  La figura 2.14 detalla el proceso de divisiones sucesivas entre 8. El número decimal 498 se divide primero entre 8, dando como resultado un cociente de 62 y un residuo de 2. El residuo (2) se convierte en el LSB del número octal. El cociente (62 en este ejemplo) se transfiere a dividendo y se divide entre 8. Esto da como resultado un cociente de 7, con un residuo de 6. El 6 se convierte en el siguiente dígito del número octal. El último cociente (7 en este ejemplo) se transfiere al dividendo y se divide entre 8. El cociente es 0 con un residuo de 7. El 7 es el dígito más significativo (MSB) del número octal. En la figura 2.14 se muestra el proceso de divisiones sucesivas entre 8 que convierte el 49810 en el equivalente octal 7628. Observe que la señal que indica el momento en que debe finalizar el proceso de las divisiones sucesivas entre 8 es cuando el cociente se hace 0. 

Figura 2.14

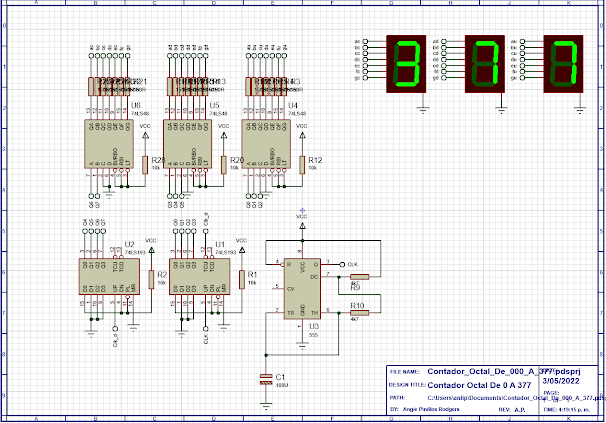
El diagrama muestra un contador octal de 000 hasta 377

Descargar Archivo