Números Hexadecimales

 SISTEMA NUMÉRICO HEXADECIMAL

El sistema de numeración hexadecimal tiene una raíz de 16. Se denomina sistema de numeración en base 16. Utiliza los símbolos 0-9, A, B, C, D, E y F como se muestra en la columna hexadecimal de la tabla de la Figura 1.7. La letra A se utiliza para el 10, la B para el 11, la C para el 12, la D para el 13, la E para el 14, y la F para el 15. La ventaja del sistema hexadecimal es que es útil para convertir directamente números binarios de 4 bits. Observar en la sección sombreada de la Figura 1.7 que cada número binario de cuatro bits, del 0000 al 1111, puede ser representado por un único dígito hexadecimal. 

Figura 1.7

Observar. la línea que corresponde al 16 en la columna decimal de la Figura 1.7. El hexadecimal equivalente es 10. Esto muestra que el sistema de numeración hexadecimal utiliza la idea de valor por posición. El 1 (en 1016) significa 16 unidades, mientras que el 0 significa cero unidades.

Convertir el número hexadecimal 2B6 en decimal. La Figura 1.8a muestra el proceso familiar. El 2 está en la posición del 256, por tanto 2 x 256 = 512, que se escribe en la línea decimal. El dígito hexadecimal B aparece en la columna del 16. Observar en la Figura 1.7 que el hexadecimal B corresponde al decimal 1l. Esto significa que hay once 16 (16 x 11), dando 176. El 176 se suma al total decimal en la parte inferior de la Figura 1.8a. La columna del 1 muestra seis 1. El 6 se suma a la línea decimal. Los valores decimales son sumados (512 + 176 + 6 = 694), dando , La Figura l.8a muestra que 2B616 es igual a 69410.

 

Figura 1.8a

Convertir el número hexadecimal A3F.C en su decimal equivalente. La Figura l.8b detalla este problema. Primero considerar la columna del 256. El dígito hexadecimal A significa que 256 debe ser multiplicado por 10, dando un producto de 2560. El número hexadecimal muestra que contiene tres 16, y por tanto 16 x 3 = 48 que se suma a la línea decimal. La columna del 1 contiene el dígito hexadecimal F, que significa 1 x 15 = 15. El 15 se suma a la línea decimal. La columna del 0.0625 contiene el dígito hexadecimal C, que significa 12 x 0.0625 = 0.75. El 0.75 se suma a la línea decimal. Al sumar los contenidos de la línea decimal (2560 + 48 + 15 + 0.75 = 2623.75) se obtiene el número decimal 2623.75. La Figura 1.8b convierte  A3F.C16 en 2623.7510

Figura 1.8b

Ahora invertir el proceso y convertir el número decimal 45 en su equivalente hexadecimal. La Figura 1.9a detalla el proceso familiar de división repetida por 16. El número decimal 45 se divide primero por 16, dando un 2 de cociente con resto 13. El resto 13 (D en hexadecimal) se convierte en el LSB del número hexadecimal. El cociente (2) se transfiere a la posición del dividendo y se divide por 16. Así se obtiene un cociente de 0 con un resto de 2. El 2 se convierte en el siguiente dígito del número hexadecimal. El proceso finaliza cuando la parte entera del cociente es 0. El proceso de la Figura 1.9a convierte el número decimal 45 en el número hexadecimal 2D.

 

Figura 1.9a

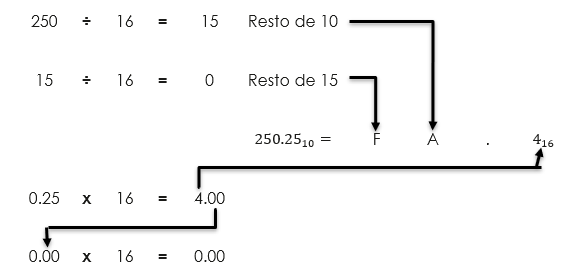
Convertir el número decimal 250.25 a hexadecimal. La conversión debe hacerse utilizando dos procesos como muestra la Figura 1.9b. La parte entera del número decimal (250) se convierte en hexadecimal utilizando el proceso de división repetida por 16. Los restos de 10 (A en hexadecimal) y 15 (F en hexadecimal) forman el número hexadecimal entero FA. La parte fraccionaria del 250.25 se multiplica por 16 (0.25 x 16). El resultado es 4.00. El entero 4 es transferido a la posición mostrada en la Figura 1.9b La conversión completa muestra que el número decimal 250.25 es igual al hexadecimal FA.4

Figura 1.9b

La principal ventaja del sistema hexadecimal es su fácil conversión al binario. La Figura 1.10a muestra el número hexadecimal 3B9 convertido a binario. Observar que cada dígito hexadecimal forma un grupo de cuatro dígitos binarios o bits. Los grupos de bits son entonces combinados para formar el número binario. En este caso 3B916 es igual a 11101110012.

 

Figura 1.10a

Otra conversión hexadecimal a binario se detalla en la Figura 1.10b. De nuevo, cada dígito hexadecimal forma un grupo de cuatro bits en el número binario. El punto hexadecimal es bajado para formar el punto binario. El número hexadecimal 47.FE se convierte en el número binario 1000111.1111111. Es claro que los números hexadecimales, debido a su compactación, son mucho más fáciles de escribir que largas cadenas de 1 y 0 en binario. El sistema hexadecimal puede considerarse como un método abreviado de escribir números binarios.

 

Figura 1.10b

La Figura 1.l0c muestra la conversión del número binario 101010000101 a hexadecimal. Primero dividir el número binario en grupos de cuatro bits comenzando en el punto binario. Cada grupo de cuatro bits se traduce a su dígito hexadecimal equivalente. La Figura 1.10c muestra que el número binario 101010000101 es igual al hexadecimal A85.

Figura 1.10c

Otra conversión binaria a hexadecimal se ilustra en la Figura 1.10d. Aquí el número binario 10010.011011 se traduce a hexadecimal. Primero el número binario se divide en grupos de cuatro bits comenzando en el punto binario. Tres 0 se añaden al grupo de más a la izquierda, formando 0001. Dos 0 se añaden al grupo de más a la derecha, formando 1100. Cada grupo tiene ahora 4 bits y se traduce a un dígito hexadecimal como muestra la Figura 1.l0d. El número binario 10010.01101 es igual a 12.6C16. 

Figura 1.10d

 

En la práctica, muchas modernas calculadoras manuales realizan conversiones entre sistemas de numeración. La mayoría pueden convertir entre decimal, hexadecimal, octal y binario. Estas calculadoras también pueden realizar operaciones aritméticas en varias bases (como por ejemplo hexadecimal).

El diagrama muestra un contador hexadecimal desde 00 hasta FF

Descargar Archivo