Compuerta Or

3.5. COMPUERTA OR (FUNCIÓN O)

     A menudo se utiliza un tipo de razonamiento que establece que, con una sola premisa que exista, existirá la conclusión. No se elimina la posibilidad de que a un mismo tiempo existan ambas premisas. Por el contrario, la concusión no existirá más que en l caso de ausencia de ambas premisas simultáneamente. 

     “Yo tomo agua cuando trabajo o estudio”. En este ejemplo “trabajo” y “estudio”, son las premisas y “tomo agua” es la conclusión. Puede apreciarse que en un momento determinado yo tomaré agua tanto si estoy trabajando como si estoy estudiando. En el caso de que trabaje y estudie al mismo tiempo, yo seguiré tomando agua. Solo dejaré de tomar agua en aquellos momentos en que no haga ni una cosa ni la otra.

3.5.1. COMPUERTA OR (FUNCIÓN O) ELEMENTAL 

     La forma más sencilla de realizar una función O de dos entradas, que llamaremos A y B, mediante componentes eléctricos, es la señalada en el circuito de la figura 3.36. 

     Partiendo de una tensión B1 de alimentación y mediante un par de interruptores, A y B, se puede encender una pequeña lámpara de denominaremos Y. 

     En el circuito se representa que si alguno de los interruptores está cerrado, la lámpara Y está encendida, el circuito realizará el siguiente razonamiento: 

     Cuando A está cerrado o B está cerrado, Y está encendida.

     Ahora; A no está cerrado, B no está cerrado, Luego Y no está encendida.

     Ahora; A no está cerrado, B sí está cerrado, Luego Y sí está encendida.

     Ahora; A sí está cerrado, B no está cerrado, Luego Y sí está encendida.

     Ahora; A sí está cerrado, B sí está cerrado, Luego Y sí está encendida. 

Figura 3.36 Circuito función O con componentes eléctricos elementales

3.5.2. COMPUERTA OR (FUNCIÓN O) A TRANSISTORES 

     Si la entrada A toma un nivel de tensión que sea ALTO, fluye corriente a través de R1, D1, diodo base-emisor de Q1 llegando por medio de R3 hasta 0V. El transistor Q1 entra en conducción y su colector alcanza una tensión lo suficientemente baja para poner a Q3 en corte. 

     Si la entrada B toma un nivel de tensión que sea ALTO, fluye corriente a través de R2, D2, diodo base-emisor de Q2 llegando por medio de R4 hasta 0V. El transistor Q2 entra en conducción y su colector alcanza una tensión lo suficientemente baja para poner a Q3 en corte. 

     En el caso de que ambas entradas, A y B tomen un nivel ALTO, entrarán al mismo tiempo en conducción los transistores Q1 y Q2, y se mantendrá el estado de corte de Q3. 

     Sin embargo, cuando la entrada A y la entrada B estén simultáneamente con un nivel de tensión BAJO, los dos transistores Q1 y Q2 estarán en corte, por no circular corriente por su diodo base-emisor, y su tensión de colector tomará un valor, lo bastante elevado para hacer que Q3 entre en estado de conducción. 

     Mientras Q3 permanece en estado de corte, su tensión de colector tomará un valor, lo bastante elevado para hacer que Q4 entre en estado de conducción y Q5 entre en estado de corte, por tanto, la salida Y tiene un nivel ALTO. 

     Mientras Q3 permanece en estado de saturación, su tensión de colector tomará un valor, lo bastante bajo para hacer que Q4 entre en estado de corte y Q5 entre en estado de saturación, por tanto, la salida Y tiene un nivel BAJO. 

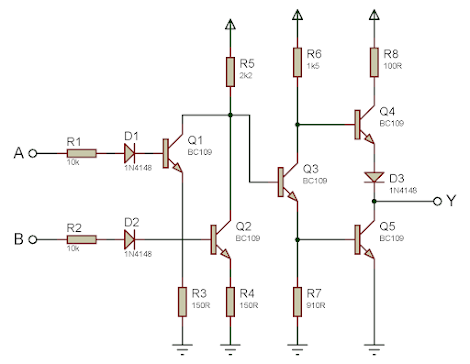
     El circuito transistorizado que realiza la función O es el correspondiente a la figura 3.37

Figura 3.37 Circuito electrónico transistorizado, que realiza la función O 

     Teniendo en cuenta los cuatro posibles casos de combinación de los niveles aplicados a las entradas A y B, los componentes del circuito se encontrarán en el siguiente estado: 

-       Cuando A = L y B = L (ambas entradas valor BAJO)

Q1 estará en corte

Q2 estará en corte

Q3 estará en saturación

Q4 estará en corte

Q5 estará en  saturación

Y = L (salida en nivel BAJO) 

-       Cuando A = L y B = H (una entrada BAJA y otra ALTA)

Q1 estará en corte

Q2 estará en saturación

Q3 estará en corte

Q4 estará en saturación

Q5 estará en  corte

Y = H (salida en nivel ALTO) 

-       Cuando A = H y B = L (una entrada ALTA y otra BAJA)

Q1 estará en saturación

Q2 estará en corte

Q3 estará en corte

Q4 estará en saturación

Q5 estará en  corte

Y = H (salida en nivel ALTO) 

-       Cuando A = H y B = H (ambas entradas en nivel ALTO)

Q1 estará en saturación

Q2 estará en saturación

Q3 estará en corte

Q4 estará en saturación

Q5 estará en  corte

Y = H (salida en nivel ALTO) 

3.5.3. OSCILOGRAMAS DE LA COMPUERTA OR (FUNCIÓN O) 

     Los oscilogramas son los gráficos correspondientes a los niveles de tensión que se aplican a las entradas de los circuitos, y que también se obtienen a la salida de éstos, en función del tiempo. 

     En la figura 3.38. se han dibujado los niveles aplicados a las entradas A y B, y el obtenido a la salida Y de un circuito lógico que es una función O, como la que se ha dibujado en la figura 3.37 

     Entre 0 y 100ns, se aplica a la entrada A un nivel BAJO y a la entrada B otro nivel BAJO. Ver parte superior y central de la figura 3.38, en este tiempo el nivel obtenido a la salida Y es, BAJO. 

     Entre 100 y 200ns, se aplica a la entrada A un nivel ALTO y a la entrada B un nivel BAJO. En este tiempo el nivel obtenido a la salida Y es, ALTO. 

     Entre 200 y 300ns, se aplica a la entrada A un nivel BAJO y a la entrada B un nivel ALTO. En este tiempo el nivel obtenido a la salida Y es, ALTO. 

     Entre 300 y 400ns, se aplica a la entrada A un nivel ALTO y a la entrada B un nivel ALTO. En este tiempo el nivel obtenido a la salida Y es, ALTO. 

Figura 3.38 Oscilograma de la compuerta OR (función O) 

3.5.4. SÍMBOLO DE LA COMPUERTA OR (FUNCIÓN O) 

     El símbolo lógico representativo de la función O se ha dibujado en la figura 3.39. Se ha puesto un ejemplo con dos entradas. 

     Como se puede apreciar, este símbolo tiene tres arcos de circunferencia que se unen formando una especie de triangulo equilátero de lados curvos. En el lado cóncavo (hundido hacia el interior), se sitúan las entradas. La salida Y de la función se toma del punto de unión de los lados convexos (hundidos hacia el exterior). 

     Recordemos que la misión del símbolo es representar, de una manera muy simplificada, una función lógica.

Figura 3.39 Símbolo de la compuerta OR (función O) 

3.5.5. TABLA DE VERDAD DE LA COMPUERTA OR (FUNCIÓN O) 

     Una función O de dos entradas A y B contendrá cuatro líneas. Cada una de estas líneas se puede asociar a uno de los casos de funcionamiento descritos en el apartado 3.5.2. y a uno de los tiempos del oscilograma que se ha dibujado en la figura 3.38 

Entradas		Salidas
B	A	Y
0	0	0
0	1	1
1	0	1
1	1	1

Figura 3.40 Tabla de verdad de la compuerta OR (función O) 

3.5.6. FÓRMULA DE LA COMPUERTA OR (FUNCIÓN O) 

     La operación realizada por la tabla de la figura 3.40 se le conoce como suma no exclusiva o simplemente suma. Se llama no exclusiva porque admite que la reunión de 1 con 1 sea igual a 1 y no a 0. 

     Debido a que nuestra función efectúa este tipo de suma, se puede decir que su fórmula es:

Y = B + A 

3.5.7. REGLAS DE SIMPLIFICACIÓN 

-       La suma admite la propiedad conmutativa. Es decir, se puede cambiar el orden de las entradas sin que por ello se altere el valor de la salida. 

B + A = A + B 

Supongamos A = 0 y B = 1, tendremos que: 

0 + 1 = 1

1 + 0 = 1 

-       En una suma en donde uno de los factores sea igual a 0, el resultado es siempre igual al otro factor o grupo de factores, si los hubiese: 

A + 0 = A 

Esta regla es válida para cualquier valor que tome A; 

Para A = 0    ; A + 0 = 0 + 0 = 0

Para A = 1    ; A + 0 = 1 + 0 = 1 

-       En una suma en donde uno de los factores sea igual a 1, el resultado es siempre igual a 1: 

A + 1 = 1 

Esta regla es válida para cualquier valor que tome A; 

Para A = 0    ; A + 1 = 0 + 1 = 1

Para A = 1    ; A + 1 = 1 + 1 = 1 

-       En una suma donde los factores son iguales, el resultado es igual siempre a uno de estos factores. Es pues: 

A + A = A 

Lo podemos comprobar dando los valores posibles al factor A. 

Para A = 0    ; A + A = 0 + 0 = 0

Para A = 1    ; A + A = 1 + 1 = 1 

-       Una suma de dos factores, en donde uno sea el inverso del otro, es siempre igual a 1. Es decir que se cumple:

 

A + A' = 1 

Lo podemos comprobar dando los valores posibles al factor A 

Para A = 0    ; A + A' = 0 + 1 = 0

Para A = 1    ; A + A' = 1 + 0 = 1 

En resumen, las leyes del álgebra booleana gobiernan la forma de operación de la puerta OR son: 

B + A = A + B

A + 0 = A

A + 1 = 1

A + A=A

A + A' = 1 

3.5.8. COMPUERTA OR (FUNCIÓN O) CON CIRCUITOS INTEGRADOS 

     Entre las características que se utilizan en las especificaciones de los circuitos integrados tenemos: 

     TA = temperatura ambiente de funcionamiento.

     En la serie 74, funcionan desde una temperatura de 0ºC, hasta temperaturas de los 70ºC 

     En la serie 54, funcionan desde una temperatura de -55ºC, hasta temperaturas de los +125ºC 

TA = 25ºC 

3.5.8.1. CIRCUITO INTEGRADO TTL 74LS32 

     Es un circuito integrado que contiene cuatro funciones O de dos entradas cada una. 

La cápsula es del tipo DIL 14, es decir, tiene 14 pines de conexión al exterior. Se alimenta con 0V por el pin 7 (GND) y con 5V (VCC) por el pin número 14. 

     Las entradas de estas funciones son los pines 1 y 2, 4 y 5, 9 y 10, 12 y 13. Las salidas respectivas son los pines 3, 6, 8 y 11. 

Figura 3.41 Distribución de pines del circuito integrado 74LS32 

     La figura 3.42 muestra la simulación de la compuerta OR TTL en el software PROTEUS 8.13. 

Figura 3.42. Circuito TTL para comprobar la compuerta OR (función O) 

3.5.8.2. CIRCUITO INTEGRADO CMOS 4071 

     El hecho de que el graduador no tenga un contacto eléctrico con el sustrato hace que los MOS adquieran ciertas características que los TTL no tienen. 

La primera de ellas es que ofrecen una muy alta impedancia de entrada, pues oscila alrededor de los  ohmios. Consecuencia de lo anterior es que consumen muy poca corriente en sus entradas. 

     Un circuito integrado CMOS que cumple con la función O se muestra en la figura 3.43. Es un circuito que se presenta bajo una capsula de 14 pines (DIL 14), que se alimenta con 0V por el pin 7 (GND) y con 15V (VDD) por el pin número 14. En su interior contiene cuatro funciones O de dos entradas cada función. Las entradas de estas funciones son los pines 1 y 2, 5 y 6, 8 y 9, 12 y 13. Las salidas respectivas son los pines 3, 4, 10 y 11.

  

Figura 3.43 Distribución de pines del circuito integrado 4071 

La figura 3.344 muestra la simulación de la compuerta OR CMOS en el software PROTEUS 8.13. 

Figura 3.43. Circuito CMOS para comprobar la compuerta OR (función O) 

3.5.9. MONTAJE EN PROTOBOARD DE UNA COMPUERTA OR 

Figura 3.44. Compuerta OR en Protoboard 

3.5.10. SIMULACIÓN DE UNA COMPUERTA OR EN PROTEUS 

3.5.11. IMPLEMENTACIÓN DE UNA COMPUERTA OR EN ISE DESIGN DE XILINX

3.5.12. IMPLEMENTACIÓN DE UNA COMPUERTA OR EN VIVADO DE XILINX